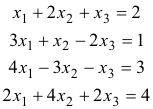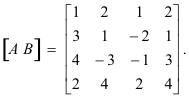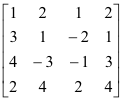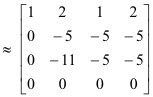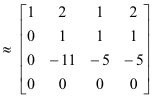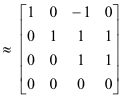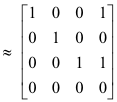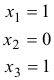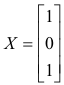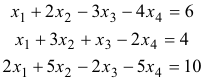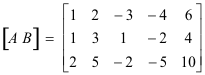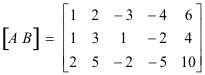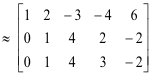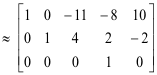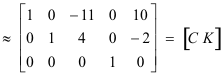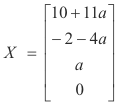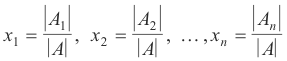Penjumlahan dan pengurangan matriks hanya dapat dilakukan apabila kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.
Matriks dapat dikalikan dengan sebuah skalar.
Matriks dapat dikalikan, dengan cara tiap baris dikalikan dengan tiap kolom, lalu dijumlahkan pada baris yang sama.
Perkalian Matriks
Anda mungkin tahu apa matriks sudah jika Anda tertarik dalam perkalian matriks. Namun, contoh cepat tidak akan menyakiti. Matriks A hanya kelompok dua-dimensi angka. Alih-alih daftar, disebut vektor, matriks adalah persegi panjang, seperti berikut:
Anda dapat mengatur variabel menjadi matriks seperti Anda dapat mengatur variabel untuk menjadi nomor satu. Dalam kasus ini, x adalah matriks yang berisi empat angka (dalam urutan tertentu). Sekarang, misalkan Anda memiliki dua matriks yang Anda butuhkan untuk berkembang biak. Perkalian untuk angka adalah sangat mudah, tapi bagaimana Anda melakukannya untuk matriks?
Berikut ini adalah titik kunci: Anda tidak bisa hanya kalikan setiap angka dengan jumlah yang sesuai dalam matriks lainnya. Perkalian matriks tidak seperti penambahan atau pengurangan. Hal ini lebih rumit, tapi proses secara keseluruhan tidak sulit untuk belajar Berikut ini adalah contoh pertama, dan kemudian aku akan menjelaskan apa yang saya lakukan.:
Contoh:

Solusi:

Anda mungkin bertanya-tanya bagaimana di dunia saya mendapat jawaban. Yah Anda dibenarkan dalam berpikir. Perkalian matriks bukanlah tugas yang mudah untuk belajar, dan Anda perlu memperhatikan untuk menghindari kesalahan ceroboh atau dua. Berikut proses:
- Langkah 1: Pindahkan di baris atas dari matriks pertama, dan bawah kolom pertama dari matriks kedua:
- Langkah 2: Kalikan setiap nomor dari baris atas dari matriks pertama dengan jumlah di kolom pertama pada matriks kedua. Dalam hal ini, itu berarti mengalikan 1 * 2 dan 6 * 9. Kemudian, mengambil jumlah dari nilai-nilai (2 54):
- Langkah 3: Masukkan nilai Anda hanya masuk ke matriks jawaban. Karena kita mengalikan baris 1 dan kolom 1, jawaban kita masuk ke yang slot di matriks jawaban:
- Langkah 4: Ulangi untuk baris dan kolom lainnya. Itu berarti Anda perlu untuk berjalan di baris pertama dari matriks pertama dan kali ini kolom kedua dari matriks kedua. Kemudian baris kedua dari matriks pertama dan kolom pertama dari kedua, dan akhirnya bagian bawah matriks pertama dan kolom kanan dari matriks kedua:
- Langkah 5: Masukkan semua nilai-nilai ke dalam matriks jawaban. Aku hanya menunjukkan Anda bagaimana untuk melakukan kiri atas dan kanan bawah. Jika Anda bekerja dua nomor lain, Anda akan mendapatkan 1 * 2 +6 * 7 = 44 dan 3 * 2 +8 * 9 = 78. Memasukkan mereka ke dalam matriks jawaban di posisi yang sesuai dan Anda mendapatkan:
Sekarang aku tahu apa yang Anda pikirkan. Itu benar-benar sulit! Yah itu akan tampak seperti itu sampai Anda terbiasa dengan proses. Ini dapat membantu Anda untuk menulis semua pekerjaan Anda, dan bahkan menarik panah untuk mengingat yang cara Anda bergerak di baris dan kolom. Hanya ingat untuk berkembang biak setiap baris dalam matriks pertama oleh setiap kolom dalam matriks kedua.
Bagaimana jika matriks tidak kotak? Kemudian Anda harus menambahkan langkah lain. Untuk mengalikan dua matriks, matriks di sebelah kiri harus memiliki kolom sebanyak matriks di sebelah kanan memiliki baris. Dengan cara itu Anda dapat menyesuaikan masing-masing pasangan saat Anda sedang mengalikan. Ukuran dari matriks akhir ditentukan oleh baris dalam matriks kiri dan kolom di sebelah kanan. Inilah yang saya lakukan:
Saya menuliskan ukuran dari matriks. Matriks kiri memiliki 2 baris dan 3 kolom, jadi itu bagaimana kita menulis itu. Baris, kolom, dalam urutan itu. Matriks lainnya adalah matriks 3x1 karena memiliki 3 baris dan hanya 1 kolom. Jika nomor di tengah cocok Anda dapat mengalikan. Angka luar memberikan ukuran jawabannya. Bahkan jika Anda mengacaukan ini, Anda akan mengetahuinya pada akhirnya karena Anda tidak akan mampu berkembang biak.
Berikut ini merupakan pengingat yang penting: Perkalian Matriks tidak komutatif. Itu berarti Anda tidak dapat beralih perintah dan mengharapkan hasil yang sama! Perkalian rutin memberitahu kita bahwa 4 * 3 = 3 * 4, tapi ini bukan perkalian dari arti biasa.
Akhirnya, inilah sebuah contoh dengan ukuran matriks yang tidak merata untuk membungkus hal-hal:
Contoh:

Jika Anda ingin bantuan lebih lanjut dengan Anda perkalian matriks, silakan untuk mengunjungi kami
matematika membantu papan pesan , atau pencarian Google untuk lebih
perkalian matriks pelajaran.
The Invers Matriks Persegi
Bilangan riil
Ketika bekerja di bilangan real, persamaan ax = b dapat diselesaikan untuk x dengan membagi kedua sisi persamaan dengan untuk mendapatkan x = b / a, asalkan tidak nol. Oleh karena itu tampaknya logis bahwa ketika bekerja dengan matriks, orang dapat mengambil persamaan matriks AX = B dan membagi kedua sisi dengan A untuk mendapatkan X = B / A.
Namun, yang tidak akan bekerja karena ...
TIDAK ada pembagian matriks!
Ok, Anda katakan. Pengurangan didefinisikan dalam hal penambahan dan pembagian didefinisikan dalam hal perkalian. Jadi, bukan membagi, saya hanya akan kalikan dengan invers. Ini adalah cara yang harus dilakukan.
Para Invers dari Matriks
Jadi, apa adalah invers dari matriks?
Nah, dalam bilangan real, kebalikan dari setiap bilangan real
a adalah nomor
satu -1, seperti
bahwa kali -1 setara dengan 1. Kami tahu bahwa untuk bilangan real, kebalikan dari jumlah itu kebalikan dari nomor tersebut, asalkan jumlahnya tidak nol.
Invers dari matriks persegi A, dinotasikan oleh A
-1, adalah matriks sehingga produk dari A dan A
-1 adalah matriks Identitas. Matriks identitas yang hasilnya akan menjadi ukuran yang sama dengan matriks A. Wow, ada banyak kesamaan antara ada bilangan real dan matriks. Itu bagus, benar - Anda tidak ingin menjadi sesuatu yang sama sekali berbeda.
A (A
-1) = I atau A
-1 (A) = I
Ada beberapa pengecualian, meskipun. Pertama-tama, A
-1 bukan berarti 1 / A. Ingat, "Tidak ada Divisi Matrix!" Kedua, Sebuah
-1 tidak berarti mengambil timbal balik dari setiap elemen dalam matriks A.
Persyaratan untuk memiliki Invers
- Matriks harus persegi (jumlah yang sama dari baris dan kolom).
- Determinan dari matriks tidak harus nol (determinan akan dibahas dalam bagian 6.4). Ini adalah bukan bilangan real tidak nol untuk memiliki invers, determinan tidak harus nol untuk memiliki invers.
Sebuah matriks bujursangkar yang memiliki invers disebut
dibalik atau
non-singular. Sebuah matriks yang tidak memiliki invers disebut
singular.
Matriks A tidak harus memiliki invers, tetapi jika tidak, kebalikannya adalah unik.
Menemukan Jalan Inverse Keras
Invers dari matriks A akan memenuhi persamaan A (A
-1) = I.
- Berdampingan matriks identitas ke kanan matriks asli, sehingga Anda memiliki A pada sisi kiri dan matriks identitas di sisi kanan. Ini akan terlihat seperti ini [A | I].
- Row-mengurangi (saya sarankan menggunakan pivoting ) matriks sampai sisi kiri adalah matriks Identitas. Ketika sisi kiri adalah matriks Identitas, sisi kanan akan Invers dengan [saya | A -1]. Jika Anda tidak dapat memperoleh matriks identitas di sisi kiri, maka matriks adalah singular dan tidak memiliki invers.
- Ambil matriks yang diperbesar dari sisi kanan dan panggilan yang kebalikannya.
Shortcut untuk Menemukan Inverse dari Matrix 2 × 2
Invers dari matriks 2 2 × dapat ditemukan dengan ...
- Mengaktifkan elemen pada diagonal utama
- Ambil kebalikan dari dua elemen lainnya
- Bagilah semua nilai dengan determinan dari matriks (karena kita belum berbicara tentang determinan, untuk sistem 2 × 2, itu adalah produk dari elemen pada diagonal utama dikurangi produk dari dua elemen lainnya).
Contoh untuk jalan pintas
Mari kita pergi dengan matriks asli
Langkah 1, switch elemen pada diagonal utama akan melibatkan switching 5 dan 7.
Langkah 2, mengambil kebalikan dari dua elemen lainnya, tapi meninggalkan mereka di mana mereka berada.
Langkah 3, mencari determinan dan membagi setiap elemen dengan itu. Determinan adalah produk dari elemen pada diagonal utama dikurangi produk dari unsur-unsur dari diagonal utama. Itu berarti determinan dari matriks ini adalah 7 (5) - (-3) (2) = 35 + 6 = 41. Kita membagi setiap elemen dengan 41.
Invers dari matriks asli ...
| 5 / 41 | 2 / 41 |
|
| -3/41 | 7 / 41 |
|
Sekarang, kau mengatakan, tunggu sebentar - Anda mengatakan tidak ada pembagian matriks. Tidak ada pembagian dengan matriks. Anda bisa mengalikan atau membagi matriks dengan skalar (bilangan real) dan determinan tersebut adalah skalar.
Menggunakan Kalkulator
Sekarang bahwa Anda tahu bagaimana menemukan matriks identitas dengan tangan, mari kita bicara kepraktisan. Kalkulator akan melakukannya untuk Anda.
Memasuki Matriks
- Tekan tombol Matrix (tepat di bawah tombol X). Di TI-83 +, Anda perlu menekan 2 Matrix nd.
- Panah untuk submenu Edit.
- Pilih Matrix untuk bekerja dengan. Anda memiliki lima untuk memilih dari dengan TI-82 dan sepuluh untuk memilih dari dengan TI-83. Biasanya, Anda akan menggunakan [A]. Cobalah untuk menghindari penggunaan [E] untuk alasan tidak jelas yang akan ditentukan jika Anda mengambil Matematika terbatas.
- Masukkan jumlah baris, tekan enter, dan kemudian masukkan jumlah kolom, diikuti oleh masukkan.
- Sekarang Anda masukkan setiap elemen dalam matriks, membaca dari kiri ke kanan dan atas ke bawah. Tekan enter setelah setiap nomor. Anda dapat menggunakan tombol panah untuk bergerak di sekitar jika Anda membuat kesalahan.
- Keluar (2 Modus nd) ketika Anda selesai memasukkan semua angka.
Menggunakan Matriks
Setiap kali Anda perlu untuk mengakses matriks yang telah Anda buat, tekan saja tombol Matrix dan memilih matriks yang sesuai. Saya menyarankan agar Anda mulai menggunakan Matrix 1, Matrix 2, dll, bukan Matrix, panah bawah, masukkan. Ini akan pergi lebih cepat, dan Anda akan melakukan banyak dengan matriks.
Mencari Invers Matrix pada suatu Kalkulator
Masukkan ekspresi [A]
-1 dengan pergi Matrix 1, dan kemudian menekan tombol x
-1. Ini tidak akan bekerja jika Anda mencoba untuk meningkatkan matriks dengan kekuatan -1 seperti dalam [A] ^ (-1).
Anda mungkin harus menggunakan tombol panah kanan atau kiri untuk menelusuri seluruh matriks untuk menuliskannya. Tolong beri jawaban yang tepat bila memungkinkan.
Salah satu cara untuk memberikan jawaban yang tepat adalah memiliki kalkulator mengkonversi desimal ke pecahan untuk Anda. Setelah semua, fraksi benar-benar teman (dan saya serius berarti bahwa di sini). Anda dapat memiliki kalkulator lakukan desimal untuk konversi fraksi oleh Math memukul, Enter, Enter.
Juga, jika Anda mendapatkan jawaban seperti 1.2E-12, kemungkinan benar-benar baik bahwa nomor adalah nol dan itu adalah karena ketidakakuratan dalam kalkulator bahwa Anda mendapatkan respon itu. Mengkonversi nomor untuk nol.
Mengapa kami perlu invers?
Saya sangat senang Anda bertanya itu.
Salah satu kegunaan utama dari invers adalah untuk memecahkan sistem persamaan linear. Anda dapat menulis sebuah sistem dalam bentuk matriks sebagai AX = B.
Sekarang, pra-kalikan kedua sisi dengan invers dari A. Pastikan Anda memenuhi dua kondisi.
- Anda harus menempatkan invers dari matriks berdekatan dengan matriks. Itu karena Invers perlu samping satu sama lain (sangat longgar matematis, tapi berpikir kembali ke fungsi) untuk membatalkan satu sama lain.
- Jika Anda kalikan dengan meletakkan sesuatu di depan sisi kiri (pra-kalikan), telah pergi di depan sisi kanan. Jika Anda menempatkan sesuatu di belakang (pasca-kalikan) sisi kiri, ia harus pergi di belakang sisi kanan.
Perkalian matriks adalah komutatif TIDAK!
Sebuah -1 (AX) = A -1 (B) ... pra-kalikan kedua sisi oleh A -1
(A -1 A) X = A -1 B ... menggunakan properti asosiatif untuk berkumpul kembali faktor-faktor
IX = A -1 B ... ketika Anda kalikan invers bersama-sama, mereka menjadi matriks identitas
X = A -1 B ... matriks identitas adalah seperti mengalikan dengan 1.
Jika AX = B, maka X = A -1 B
Jadi apa yang Anda minta dengan cara yang normal sinis Anda adalah, "Anda baru saja memecahkan persamaan yang lain, apa yang harus dilakukan dengan sesuatu?"
Memecahkan Sistem Persamaan Linear
Perhatikan sistem persamaan linear
3x + 2y - 5z = 12
x - 3y + 2z = -13
5x - y + 4z = 10
Tulis koefisien dalam matriks A.
| x | y | z |
|
|---|
| 3 | 2 | -5 |
|
| 1 | -3 | 2 |
|
| 5 | -1 | 4 |
|
Tulis variabel dalam matriks X.
Tulis konstanta dalam matriks B.
Pastikan bahwa AX = B
Langkah ini tidak benar-benar dibutuhkan, tapi aku ingin menunjukkan padamu bahwa hal ini benar-benar bekerja.
AX akan menjadi (3 × 3) × (3 × 1) = 3 × 1 matriks. Matriks B juga 3 × 1 matriks, jadi setidaknya dimensi berjalan dengan baik.
Berikut Sebuah X. kali
| 3 | 2 | -5 |
|
|
| x |
|
|
| 3x + 2y - 5z |
|
| 1 | -3 | 2 |
|
|
| y |
| = |
| 1x - 3y + 2z |
|
| 5 | -1 | 4 |
|
|
| z |
|
|
| 5x - 1thn + 4z |
|
Perhatikan bahwa ternyata sisi kiri dari sistem persamaan. B adalah sisi kanan, jadi kami telah mencapai kesetaraan. Yak! Anda dapat menulis sebuah sistem persamaan linear AX = B. sebagai
Jadi, jika Anda dapat menulis sebuah sistem persamaan linear AX = B di mana A adalah matriks koefisien, X adalah matriks variabel, dan B adalah sisi kanan, Anda dapat menemukan solusi untuk sistem dengan X = A
-1 B.
Tempatkan ke dalam matriks koefisien [A] pada kalkulator dan sisi kanan ke [B].
Jika Anda bertanya kalkulator untuk mencari invers dari matriks koefisien, itu akan memberi Anda ini untuk A
-1
| 5 / 44 | 3 / 88 | 1 / 8 |
|
| -3/44 | -37/88 | 1 / 8 |
|
| -7/44 | -13/88 | 1 / 8 |
|
Anda bisa melakukan itu, dan kemudian kalikan dengan B, tapi akan lebih mudah hanya untuk menempatkan seluruh ekspresi ke dalam kalkulator dan mendapatkan jawaban langsung. Bahkan apa yang ditunjukkan di bawah ini adalah pekerjaan lebih dari yang diperlukan.
X = A
-1 B = ...
| x |
|
|
| 5 / 44 | 3 / 88 | 1 / 8 |
|
|
| 12 |
|
|
| 191/88 |
|
| y |
| = |
| -3/44 | -37/88 | 1 / 8 |
|
|
| -13 |
| = |
| 519/88 |
|
| z |
|
|
| -7/44 | -13/88 | 1 / 8 |
|
|
| 10 |
|
|
| 111/88 |
|
Di sana Anda pergi, x = 191/88, y = 519/88, dan z = 111/88. Itu akan menjadi sakit nyata untuk memecahkan dengan tangan.
Sistem persamaan linear. Solusi matriks, matriks, sistem homogen dan non-homogen, aturan Cramer, ruang nol
Matriks bentuk sistem linear persamaan. Bentuk matriks dari sistem m persamaan linear dengan n variabel tidak diketahui
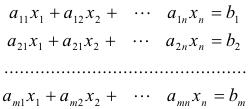
adalah



atau, lebih ringkas,
AX = B
dimana A adalah matriks koefisien,
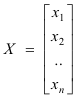
dan

.
Matriks dari sistem persamaan linear. Matriks yang diperbesar dari sistem persamaan linear AX = B adalah matriks

dibentuk dengan menambahkan vektor konstan (yang b) di sebelah kanan dari matriks koefisien.
Memecahkan sistem persamaan linear dengan mengurangi matriks yang diperbesar dari sistem menjadi bentuk kanonis baris. Suatu sistem persamaan linear AX = Y dapat diselesaikan dengan mengurangi matriks yang diperbesar dari sistem menjadi bentuk kanonis baris oleh operasi baris elementer.
Contoh. Memecahkan sistem
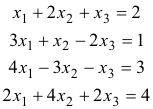
Matriks yang diperbesar adalah
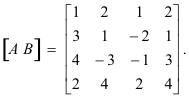
[AB] dikurangi dengan transformasi baris elementer menjadi bentuk kanonis baris setara sebagai berikut:
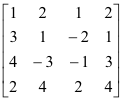
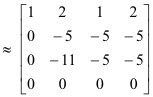
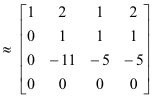
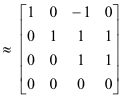
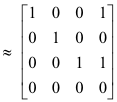
Jadi solusinya adalah sistem persamaan:
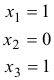
Disajikan dalam bentuk vektor, kami telah
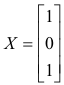 Teorema Dasar
Teorema Dasar
Bagaimana seseorang tahu apakah sistem m persamaan linear dengan n variabel tidak diketahui adalah yaitu konsisten atau tidak konsisten jika memiliki solusi atau tidak? Jawabannya diberikan oleh teorema fundamental berikut.
Teorema fundamental. Sebuah sistem AX = B m persamaan linear dengan n variabel tidak diketahui adalah konsisten jika dan hanya jika matriks koefisien dan matriks yang diperbesar dari sistem memiliki rank yang sama.
Bukti.
Corollary Kondisi yang diperlukan untuk sistem AX = B n + 1 persamaan linear dalam n variabel tidak diketahui memiliki solusi adalah |. AB | = 0 yaitu determinan dari matriks yang diperbesar sama dengan nol.
Teorema. Dalam sistem yang konsisten AX = B m persamaan linear dengan n variabel tidak diketahui peringkat r <n, nr yang tidak diketahui dapat dipilih sehingga matriks koefisien yang tidak diketahui r tersisa adalah peringkat r. Ketika diketahui nr ditugaskan nilai-nilai apa pun, tidak diketahui r lainnya ditentukan secara unik.
Contoh. Dalam sistem
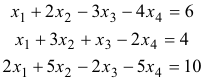 matriks yang diperbesar adalah
matriks yang diperbesar adalah
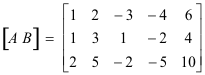 Kami mengurangi [AB] dengan transformasi baris elementer menjadi bentuk kanonis baris setara [CK] sebagai berikut:
Kami mengurangi [AB] dengan transformasi baris elementer menjadi bentuk kanonis baris setara [CK] sebagai berikut:
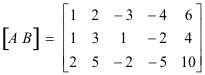
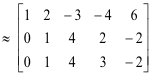
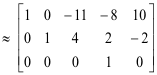
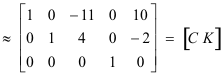 Karena A dan [AB] masing-masing peringkat r = 3, sistem yang diberikan konsisten, apalagi, solusi umum mengandung n - r = 4 - 3 = 1 konstanta sembarang. Dari baris terakhir [CK],
Karena A dan [AB] masing-masing peringkat r = 3, sistem yang diberikan konsisten, apalagi, solusi umum mengandung n - r = 4 - 3 = 1 konstanta sembarang. Dari baris terakhir [CK], 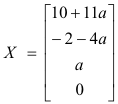 = 0. Mari
= 0. Mari 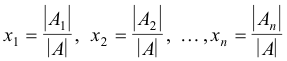 = Dimana adalah sewenang-wenang, kemudian
= Dimana adalah sewenang-wenang, kemudian 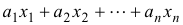 = 10 + 11a dan
= 10 + 11a dan 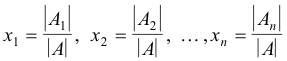 = -2 - 4a .. Solusi dari sistem diberikan oleh
= -2 - 4a .. Solusi dari sistem diberikan oleh 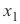 = 10 + 11a,
= 10 + 11a,  = -2 - 4a,
= -2 - 4a, 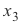 = A,
= A, 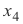 = 0 atau
= 0 atau
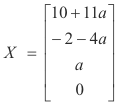 Homogen dan non homogen sistem. Sebuah persamaan linear dari jenis
Homogen dan non homogen sistem. Sebuah persamaan linear dari jenis
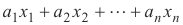 = 0
di mana suku konstanta adalah nol disebut homogen sedangkan persamaan linear dari jenis
= 0
di mana suku konstanta adalah nol disebut homogen sedangkan persamaan linear dari jenis
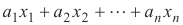 = B
dimana b Istilah konstan tidak nol adalah disebut non-homogen. Demikian pula sistem persamaan AX = 0 disebut homogen dan sistem AX = B adalah disebut non-homogen B yang diberikan tidak vektor nol.
Teorema. Sebuah sistem non-homogen n persamaan dengan n variabel tidak diketahui AX = B memiliki solusi unik yang disediakan rank dari matriks koefisien A adalah n, yang disediakan
= B
dimana b Istilah konstan tidak nol adalah disebut non-homogen. Demikian pula sistem persamaan AX = 0 disebut homogen dan sistem AX = B adalah disebut non-homogen B yang diberikan tidak vektor nol.
Teorema. Sebuah sistem non-homogen n persamaan dengan n variabel tidak diketahui AX = B memiliki solusi unik yang disediakan rank dari matriks koefisien A adalah n, yang disediakan 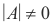 .
Dua tambahan metode untuk memecahkan sistem non-homogen AX = B yang konsisten dari n persamaan dalam n variabel tidak diketahui.
Metode determinan menggunakan Peraturan Cramers itu. Dinotasikan dengan
.
Dua tambahan metode untuk memecahkan sistem non-homogen AX = B yang konsisten dari n persamaan dalam n variabel tidak diketahui.
Metode determinan menggunakan Peraturan Cramers itu. Dinotasikan dengan 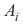 , (I = 1,2, ..., n) matriks yang diperoleh dari A dengan mengganti kolom ke-i dengan kolom konstanta (b itu). Kemudian, jika | A |
, (I = 1,2, ..., n) matriks yang diperoleh dari A dengan mengganti kolom ke-i dengan kolom konstanta (b itu). Kemudian, jika | A | 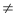 0, sistem AX = B memiliki solusi unik
0, sistem AX = B memiliki solusi unik
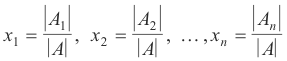 Solusi menggunakan A -1. Jika | A |
Solusi menggunakan A -1. Jika | A | 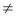 0, Sebuah -1 ada dan solusi dari sistem AX = B diberikan oleh X = A -1 B
Sistem persamaan homogen.
Perhatikan sistem persamaan linear homogen AX = 0 yang terdiri dari m persamaan dengan n variabel tidak diketahui. Biarkan rank dari matriks koefisien A r. Jika r = n solusinya hanya terdiri dari solusi tunggal X = 0, yang disebut solusi trivial. Jika r <n ada jumlah tak terbatas vektor solusi yang akan memenuhi sistem yang sesuai untuk semua titik dalam beberapa subruang n-dimensi ruang. Untuk menggambarkan ini mari kita perhatikan beberapa contoh sederhana dari biasa tiga-dimensi ruang.
Misalkan AX sistem = 0 terdiri dari persamaan tunggal
5x + 3y + 9z = 0
Persamaan ini sesuai dengan pesawat dalam tiga dimensi ruang yang melewati asal sistem koordinat. Setiap titik pada pesawat ini memenuhi persamaan tersebut dan dengan demikian solusi untuk AX = 0 sistem kami. Himpunan semua solusi untuk AX = 0 sistem kami sesuai dengan semua titik pada pesawat ini. Selanjutnya, sejak pesawat melewati asal sistem koordinat, pesawat merupakan ruang vektor. Mengapa? Karena kombinasi linear dari dua vektor dalam pesawat juga di pesawat dan setiap vektor di pesawat dapat diperoleh sebagai kombinasi linear dari dua vektor setiap dasar dalam pesawat. Jadi, dalam ringkasan, dalam contoh khusus ini solusi set ke AX = 0 sistem kami sesuai dengan subruang dua dimensi dari ruang tiga dimensi diwakili oleh pesawat ini. Kami menyebutnya ruang bagian ruang solusi dari AX = 0 sistem.
Mari kita perhatikan contoh lain. Misalkan AX = 0 sistem terdiri dari dua persamaan berikut
2x + 5y + 3z = 0
9x - 2y - 8z = 0
Kedua persamaan sesuai dengan dua pesawat dalam tiga dimensi ruang yang bersinggungan dalam beberapa garis yang melewati titik asal dari sistem koordinat. Setiap titik ini garis persimpangan memenuhi sistem dan dengan demikian solusi untuk AX = 0 sistem kami. Selanjutnya, karena garis melewati titik asal dari sistem koordinat, garis merupakan ruang vektor. Kombinasi linear dari dua vektor dalam setiap baris juga sejalan dan setiap vektor di baris dapat diperoleh sebagai kombinasi linear dari setiap vektor basis untuk baris. Jadi, dalam ringkasan, dalam contoh ini solusi set ke AX = 0 sistem kami sesuai dengan subruang satu dimensi dari ruang tiga dimensi diwakili oleh garis perpotongan dari dua pesawat. Dalam hal ini ruang solusi dari sistem AX = 0 adalah satu-dimensi.
Apa yang menentukan dimensi dari ruang solusi dari AX sistem = 0? Dimensi diberikan oleh n - r. Dalam contoh pertama kita jumlah tidak diketahui, n, 3 dan pangkat, r, adalah 1 sehingga dimensi dari ruang solusi adalah 3 - 1 = 2. Dalam contoh kedua kami n = 3 dan r = 2 sehingga dimensi dari ruang solusi adalah 3 - 2 = 1.
Null ruang matriks. Ruang solusi dari sistem homogen AX = 0 disebut ruang nol dari matriks A. Alasan untuk nama ini adalah bahwa jika matriks A dipandang sebagai suatu operator linear yang memetakan titik dari beberapa ruang vektor V ke dalam dirinya sendiri, dapat dilihat sebagai pemetaan semua unsur ini ruang solusi dari AX = 0 menjadi elemen nol "0". Jadi ruang nol U dari A adalah ruang bagian dari semua vektor di V yang dicitrakan dalam elemen nol "0" oleh matriks A.
Nulitas dari suatu matriks. Nulitas dari matriks A adalah dimensi dari ruang nol A.
Jika matriks A memiliki nulitas s, maka AX = 0 memiliki solusi independen linear s X 1, X 2, ... , X s sehingga setiap solusi dari AX = 0 adalah kombinasi linear dari mereka dan setiap kombinasi linear dari mereka adalah solusi. Sebuah basis untuk ruang nol adalah setiap set solusi s linear dari AX = 0. Nulitas dari matriks mxn dengan rank r diberikan oleh
s = n - r.
Teorema 1. Kondisi yang diperlukan dan cukup untuk sistem AX = 0 memiliki solusi selain solusi trivial adalah bahwa rank dari A adalah r <n.
Teorema 2 Sebuah kondisi yang perlu dan cukup bahwa sistem AX = 0 n persamaan homogen dalam diketahui memiliki solusi selain solusi trivial adalah |. A | = 0.
Teorema 3. Jika peringkat dari AX = 0 adalah r <n, sistem memiliki tepat nr solusi linear independen seperti bahwa solusi setiap kombinasi linear dari nr solusi bebas linear dan setiap kombinasi linier tersebut adalah solusi.
Lengkap solusi dari sistem homogen AX = 0.
Solusi lengkap dari AX = 0 sistem linear dari m persamaan dengan n variabel tidak diketahui terdiri dari ruang nol dari A yang dapat diberikan sebagai semua kombinasi linear dari setiap himpunan vektor-vektor bebas linear yang mencakup ruang nol. Jika rank dari A adalah r, akan ada nr vektor bebas linear
0, Sebuah -1 ada dan solusi dari sistem AX = B diberikan oleh X = A -1 B
Sistem persamaan homogen.
Perhatikan sistem persamaan linear homogen AX = 0 yang terdiri dari m persamaan dengan n variabel tidak diketahui. Biarkan rank dari matriks koefisien A r. Jika r = n solusinya hanya terdiri dari solusi tunggal X = 0, yang disebut solusi trivial. Jika r <n ada jumlah tak terbatas vektor solusi yang akan memenuhi sistem yang sesuai untuk semua titik dalam beberapa subruang n-dimensi ruang. Untuk menggambarkan ini mari kita perhatikan beberapa contoh sederhana dari biasa tiga-dimensi ruang.
Misalkan AX sistem = 0 terdiri dari persamaan tunggal
5x + 3y + 9z = 0
Persamaan ini sesuai dengan pesawat dalam tiga dimensi ruang yang melewati asal sistem koordinat. Setiap titik pada pesawat ini memenuhi persamaan tersebut dan dengan demikian solusi untuk AX = 0 sistem kami. Himpunan semua solusi untuk AX = 0 sistem kami sesuai dengan semua titik pada pesawat ini. Selanjutnya, sejak pesawat melewati asal sistem koordinat, pesawat merupakan ruang vektor. Mengapa? Karena kombinasi linear dari dua vektor dalam pesawat juga di pesawat dan setiap vektor di pesawat dapat diperoleh sebagai kombinasi linear dari dua vektor setiap dasar dalam pesawat. Jadi, dalam ringkasan, dalam contoh khusus ini solusi set ke AX = 0 sistem kami sesuai dengan subruang dua dimensi dari ruang tiga dimensi diwakili oleh pesawat ini. Kami menyebutnya ruang bagian ruang solusi dari AX = 0 sistem.
Mari kita perhatikan contoh lain. Misalkan AX = 0 sistem terdiri dari dua persamaan berikut
2x + 5y + 3z = 0
9x - 2y - 8z = 0
Kedua persamaan sesuai dengan dua pesawat dalam tiga dimensi ruang yang bersinggungan dalam beberapa garis yang melewati titik asal dari sistem koordinat. Setiap titik ini garis persimpangan memenuhi sistem dan dengan demikian solusi untuk AX = 0 sistem kami. Selanjutnya, karena garis melewati titik asal dari sistem koordinat, garis merupakan ruang vektor. Kombinasi linear dari dua vektor dalam setiap baris juga sejalan dan setiap vektor di baris dapat diperoleh sebagai kombinasi linear dari setiap vektor basis untuk baris. Jadi, dalam ringkasan, dalam contoh ini solusi set ke AX = 0 sistem kami sesuai dengan subruang satu dimensi dari ruang tiga dimensi diwakili oleh garis perpotongan dari dua pesawat. Dalam hal ini ruang solusi dari sistem AX = 0 adalah satu-dimensi.
Apa yang menentukan dimensi dari ruang solusi dari AX sistem = 0? Dimensi diberikan oleh n - r. Dalam contoh pertama kita jumlah tidak diketahui, n, 3 dan pangkat, r, adalah 1 sehingga dimensi dari ruang solusi adalah 3 - 1 = 2. Dalam contoh kedua kami n = 3 dan r = 2 sehingga dimensi dari ruang solusi adalah 3 - 2 = 1.
Null ruang matriks. Ruang solusi dari sistem homogen AX = 0 disebut ruang nol dari matriks A. Alasan untuk nama ini adalah bahwa jika matriks A dipandang sebagai suatu operator linear yang memetakan titik dari beberapa ruang vektor V ke dalam dirinya sendiri, dapat dilihat sebagai pemetaan semua unsur ini ruang solusi dari AX = 0 menjadi elemen nol "0". Jadi ruang nol U dari A adalah ruang bagian dari semua vektor di V yang dicitrakan dalam elemen nol "0" oleh matriks A.
Nulitas dari suatu matriks. Nulitas dari matriks A adalah dimensi dari ruang nol A.
Jika matriks A memiliki nulitas s, maka AX = 0 memiliki solusi independen linear s X 1, X 2, ... , X s sehingga setiap solusi dari AX = 0 adalah kombinasi linear dari mereka dan setiap kombinasi linear dari mereka adalah solusi. Sebuah basis untuk ruang nol adalah setiap set solusi s linear dari AX = 0. Nulitas dari matriks mxn dengan rank r diberikan oleh
s = n - r.
Teorema 1. Kondisi yang diperlukan dan cukup untuk sistem AX = 0 memiliki solusi selain solusi trivial adalah bahwa rank dari A adalah r <n.
Teorema 2 Sebuah kondisi yang perlu dan cukup bahwa sistem AX = 0 n persamaan homogen dalam diketahui memiliki solusi selain solusi trivial adalah |. A | = 0.
Teorema 3. Jika peringkat dari AX = 0 adalah r <n, sistem memiliki tepat nr solusi linear independen seperti bahwa solusi setiap kombinasi linear dari nr solusi bebas linear dan setiap kombinasi linier tersebut adalah solusi.
Lengkap solusi dari sistem homogen AX = 0.
Solusi lengkap dari AX = 0 sistem linear dari m persamaan dengan n variabel tidak diketahui terdiri dari ruang nol dari A yang dapat diberikan sebagai semua kombinasi linear dari setiap himpunan vektor-vektor bebas linear yang mencakup ruang nol. Jika rank dari A adalah r, akan ada nr vektor bebas linear 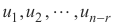 yang menjangkau ruang nol A. Jadi solusi lengkap dapat ditulis sebagai
X =
yang menjangkau ruang nol A. Jadi solusi lengkap dapat ditulis sebagai
X = 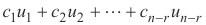 mana
mana 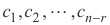 adalah konstanta sembarang.
Lengkap solusi dari sistem non-homogen AX = B.
Jika sistem AX = B dari m persamaan dengan n variabel tidak diketahui konsisten, solusi lengkap dari sistem diberikan oleh solusi lengkap dari AX = 0 ditambah solusi khusus dari AX = B. solusi lengkap dari AX = 0 terdiri dari ruang nul dari A yang dapat diberikan sebagai semua kombinasi linear dari setiap himpunan vektor-vektor bebas linear yang mencakup ruang nol. Jika rank dari A adalah r, akan ada nr vektor bebas linear
adalah konstanta sembarang.
Lengkap solusi dari sistem non-homogen AX = B.
Jika sistem AX = B dari m persamaan dengan n variabel tidak diketahui konsisten, solusi lengkap dari sistem diberikan oleh solusi lengkap dari AX = 0 ditambah solusi khusus dari AX = B. solusi lengkap dari AX = 0 terdiri dari ruang nul dari A yang dapat diberikan sebagai semua kombinasi linear dari setiap himpunan vektor-vektor bebas linear yang mencakup ruang nol. Jika rank dari A adalah r, akan ada nr vektor bebas linear 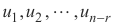 yang menjangkau ruang nol A. Jika kita menunjukkan solusi tertentu dari AX = B dengan
yang menjangkau ruang nol A. Jika kita menunjukkan solusi tertentu dari AX = B dengan 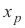 maka solusi lengkap dapat ditulis sebagai
X =
maka solusi lengkap dapat ditulis sebagai
X = 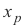 +
+ 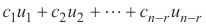 mana
mana 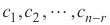 adalah konstanta sembarang.
adalah konstanta sembarang.
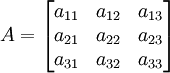


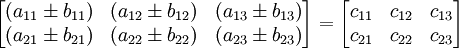
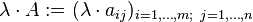


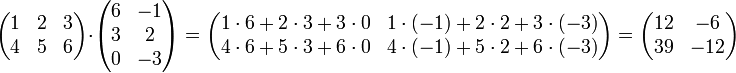








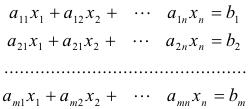


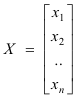
 .
.